Film I.1. A bouncing droplet in slow motion
Slow motion movie of a millimeter size drop as it bounces on the surface of a bath of the same fluid oscillated vertically. The fluid is a silicon oil with viscosity μL=20×10-3Pas. The oscillation frequency is 80 Hz.
Bouncing droplets
Normally, a liquid drop falling on a bath of the same liquid disappears rapidly (a few tenths of a second). This coalescence however, is slightly delayed by the need for air to flow out of the intermediate region. As this air film thins down, a van der Waals attractive force brings the two fluids into contact. As soon as this contact is effective, surface tension leads to a minimization of the interface area and to merging. Several situations are known in which this merging is delayed. In particular it was shown by K.R. Sreenivas et al. [ref 1] that in the vicinity of a hydraulic jump a lubrication effect could generate a lift strong enough to keep the drop sustained. Investigating this effect during an undergraduate student project at University Paris Diderot, we found that the coalescence could also be inhibited if the bath was vibrated vertically with a characteristic acceleration exceeding gravity [P1]. In these conditions, as shown on the first video, a droplet bounces periodically on the interface. Each time the droplet collides with the bath, it remains separated from it by a continuous air film. Before this air film has time to break, the drop lifts off again. A silicon oil droplet of millimetre size can thus be maintained for an unlimited time (several days if needed) in a kind of "oscillating levitation" on the liquid surface.It can be noticed that a capillary surface wave is generated at each collision of the drop with the bath. It is the source of the interaction of drops bouncing on the same interface (see crystals) as well as that of the propagation of a single drop (see walkers)
Film I.2. The simplest way to create a bouncing droplet
In order to obtain drops of a controlled size, we dip a conical pin (typically a tooth pick) into the vibrating bath and remove it swiftly [Protière et al. 2006]. The breaking of the resulting liquid bridge between the bath and the pin generates a single drop. Its size is a simple function of the initial immersion depth of the cone tip. The diameter of the drop is then checked by optical means. Drops with a controlled size can be obtained by forcing an oil jet with a piezo-electric quartz as shown by Terwagne et al [ref 2]
The various regimes of bouncing and the transition to walking
The dynamics of the bouncing of a given droplet evolves when the amplitude of oscillation of the bath is increased as shown in Fig. I.1 (a-c). This evolution depends on the drop size and we established in our early investigations [P4 and T1] phase diagrams of the type shown in Fig. I.1 (d) that summarize the main regimes of the drop bouncing behaviour.
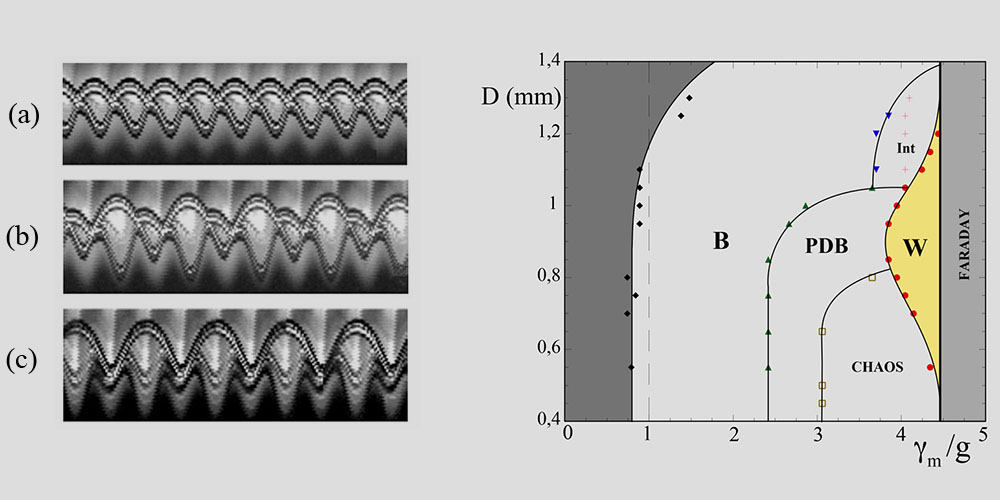
Fig. I.1.
The diagram shown in Fig 1-1 [P4] corresponds to the various bouncing regimes obtained at a fixed forcing frequency on a given fluid. Similar behaviours can be obtained with other fluids for other frequencies and drops of different sizes.
The modelling of the various regimes of bouncing requires refined fluid dynamics analyses, [ref 2-5] taking into account the deformation of the drop, that of the interface and a model for the interstitial air flow. The result of Moláček and Bush show that their model is precise enough to account for all the transitions between the different bouncing regimes in phase diagrams that turn out to be more complex than that shown in Fig 1-1.
(a-c) Spatio-temporal recordings showing the evolution of the bouncing when the amplitude of the vertical oscillation is increased.
(d) The corresponding phase diagram [P4] showing the main bouncing regimes of droplets as a function of their diameter D and the forcing acceleration. The fluid is a silicon oil of viscosity μ=50×10-3Pas and the forcing frequency is f0=50Hz. For weak values of γm/g, the drops do not lift from the surface and coalesce with the substrate (grey region). In region B, the drops bounce at the forcing frequency as shown in (a). For larger imposed acceleration (region DPD) their vertical motion becomes sub-harmonically modulated as shown in (b). In the region W, the period doubling is complete and the drop touches the interface only once in two periods as shown in (c). Correspondingly, it becomes propagative. For larger forcing, in the grey band to the right, the whole fluid surface is destabilized by the Faraday instability.
Film I.3. Period doubled bouncing and transition to walk
The evolution of the bouncing for increasing forcing amplitudes showing the transition to a complete period doubling and to walking.
Bibliography
Publications
[P1] From Bouncing to Floating : Noncoalescence of Drops on a Fluid Bath (PDF)
Y. Couder, E. Fort, C.-H. Gautier, and A. BoudaoudPhys. Rev. Lett. 94, 177801 (2005)
[P4] Particle-wave association on a fluid interface (PDF)
S. Protière, A. Boudaoud and Yves CouderJ. Fluid Mech. 554, 85-108 (2006).
Thesis
[T1] Gouttes rebondissantes : une association onde-particule à échelle macroscopique (PDF)
Suzie Protière, Thèse de Doctorat de l’Université Paris-Diderot, 25 octobre 2007
References
[ref 1] Levitation of a drop over a film flow
Sreenivas, K. R. , De P. K., and Arakeri J. H.,J. Fluid Mech 380, 297 (1999)
[ref 2] A quasi-static model of a drop impact
Moláček J and Bush J W MPhys. Fluids 24, 127103 (2012)
[ref 3] The role of the droplet deformation in the droplet bouncing dynamics
Terwagne D., Ludewig T., Vandewalle N. and Dorbolo S.,Phys. Fluids 25, 122101 (2013)
[ref 4] Drops bouncing on a vibrated bath
Moláček J and Bush J W MJ. Fluid Mech. 727, 582-611 (2013)
[ref 5] Pilot-wave hydrodynamics
Bush, J.W.MAnn. Rev. Fluid Mech. 49, 269-292 (2015).
