Film II.1. A 2D crystal of bouncing droplets
Crystals with Simple Bouncing
When several droplets coexist on the same vibrated bath, the interface is disturbed by the waves they generate. This creates a long-distance interaction between the drops. When initially randomly distributed, they are observed to drift slowly with time because each of them receives non-vertical kicks as it collides with a slanted the interface. This wave-mediated interaction leads to the formation of 2D crystal like structures [P3, P10] (or to that of self-propelled droplet aggregates [P7]). A crystal is formed once all droplets have found an equilibrium position in locations where the average slope during contact is zero [P10]. They are thus observed to occupy the antinodes of a global stationary wave-field sustained by their bouncing. In the most stable arrangements, each droplet settles at the first antinode of the wave generated by its nearest neighbours. For drops bouncing at the forcing frequency this leads to the spontaneous formation of aggregates with a crystalline triangular order as shown in films II.1, II.2 and II.3. The resulting structure forms an original 2D mass-spring periodic array.


Films II.2 & II.3. An elementary crystalite
Slow motion of seven droplets forming a small aggregate with triangular lattice as seen from the side and the top
Crystals with Period Doubled Bouncing
For larger forcing amplitudes, as described above, the vertical bouncing becomes sub-harmonically modulated. During two successive periods of forcing a given drop undergoes one strong and one weak collision with the interface. Only the former is efficient in emitting waves so that the main phenomena have a period double that of forcing. On the bath thus coexist two types of droplets that bounce with opposite phases. For large forcing, the waves also become less damped. These two effects increase the variety of possible distances of binding [P10]. In this situation other crystalline structures form, the simplest of them being a square crystal formed of two sub-lattices of drops each bouncing with its own phase (see films II.4, and II.5).

Film II.4. Square crystal
Slow motion of droplets with period doubled bouncing forming an aggregate as seen from the side. The droplets bouncing with opposite phases form two square sub-lattices.
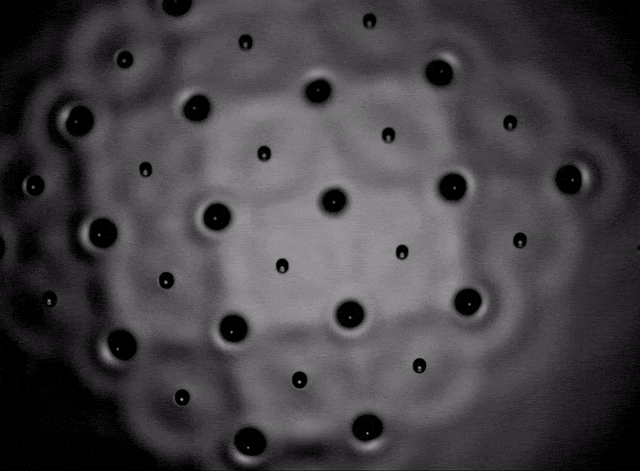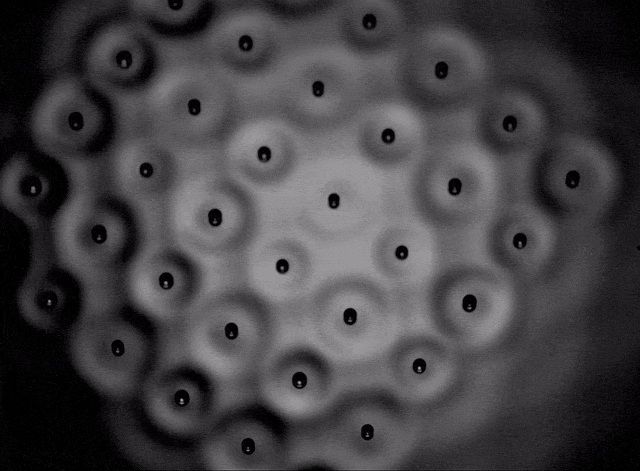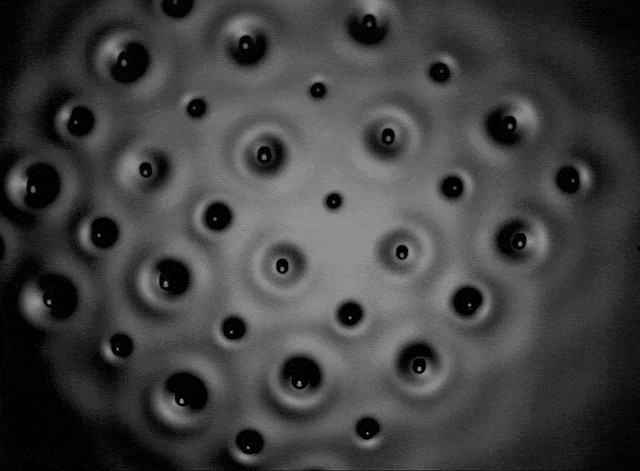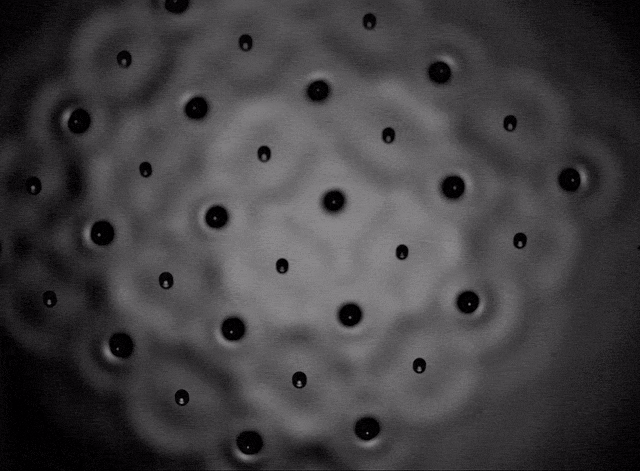
Film II.5. Square crystal
The formation of various polygonal clusters (squares, hexagons and octagons) also becomes possible and from these elementary polygons it is possible to artificially assemble crystalline structures related to the Archimedean tilings of the plane. These are the periodic tessellations first investigated by Kepler that cover uniformly the 2D plane with convex polygons. Eight of the eleven possible configurations were observed [P10]. They are stabilized by the coupling of two sub-lattices of droplets of different phase, both contributing to sustain a common wave field. Three examples are shown in films II-6, II-7, and II-8.
Slow motion of droplets of a similar square structure as seen from the top.


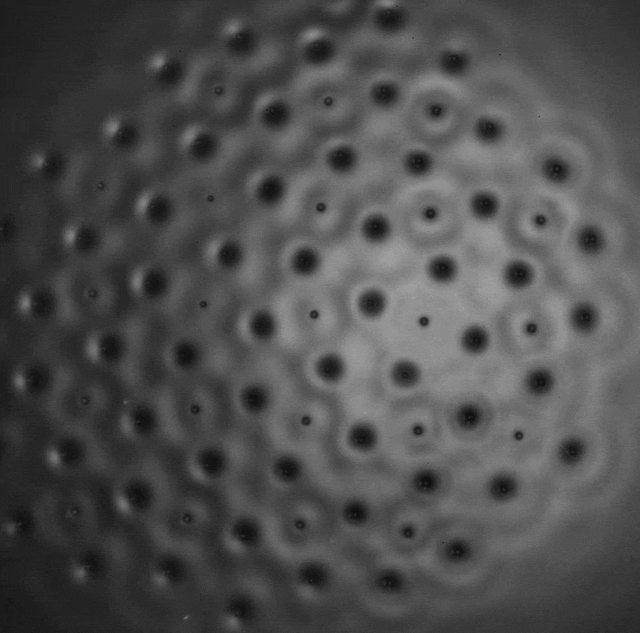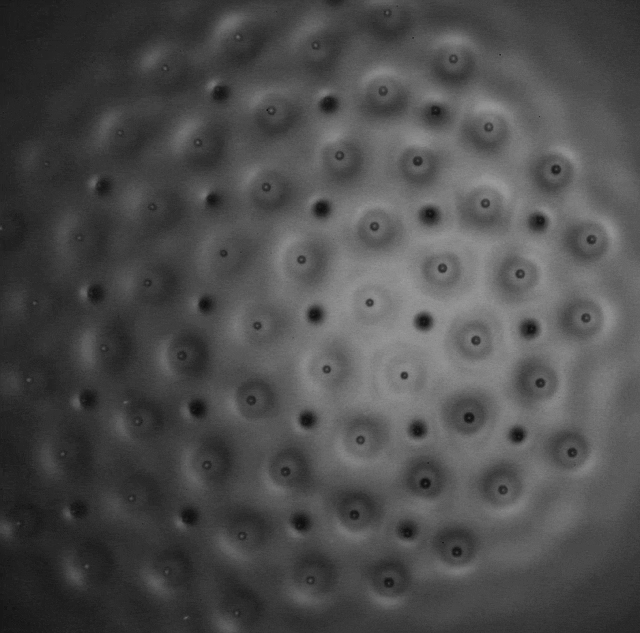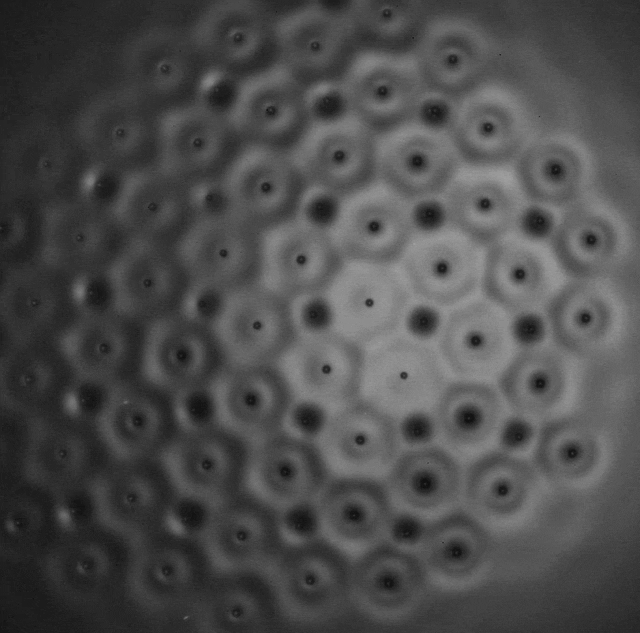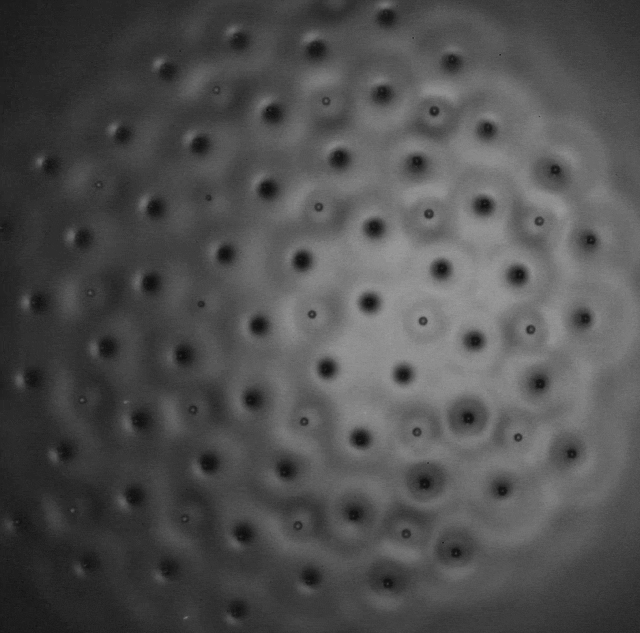
Films II.6, II.7 & II.8. Three different Archimedian tesselations
Slow motion of droplets forming an aggregate with
- truncated square sub lattice associated to a square sublattice (top)
- small rhombitrihexagonal sublattice associated to a trihexagonal sublattice (middle)
- snub square sublattice is associated to a square sublattice (bottom)
Vibrations in a Crystal
The droplets of these crystalline aggregates are massive interacting objects evolving in a potential trap given by the wave-mediated interaction. They thus form an original periodic mass-spring chain. We investigated [P13] the spontaneous instability of this periodic pattern when the forcing acceleration, used as the control parameter, is increased. Films II.9 and II.10 show the observed oscillations. The coherent vibration is reminiscent of phonons in crystalline lattices. Here however only a single value in the vibration spectrum is excited.
Films II.9 & II.10. The spontaneous oscillations of two aggregates with different lattices.
Bibliography
Publications
[P3] The self-organization of capillary wave sources (PDF)
Suzie Protière, Yves Couder, Emmanuel Fort and Arezki BoudaoudJ. Phys.: Condens. Matter 17 S3529_S3535 (2005)
[P10] Archimedean lattices in the bound states of wave interacting particles (PDF)
A. Eddi, A. Decelle, E. Fort & Y. CouderEPL, 87, 56002 (2009)
[P13] Oscillating instability in droplets crystalline aggregates (PDF)
A. Eddi, A. Boudaoud & Y.CouderEPL, 94 , 20004 (2011)
[P7] Wave propelled ratchets and drifting rafts (PDF)
A. Eddi, D. Terwagne, E. Fort and Y.CouderEPL, 82, 44001 (2008)
