A finite temporal extent
In a walker the drop being driven by the waves, a crucial asset for the system’s dynamical properties lies in the nature of this global wave field. Film IV-1 shows the very distinctive structure of the wave-field of a walker as it moves rectilinearly, far away from any boundary.Since it results from the waves emitted by the droplet during successive collisions with the interface, we needed to characterize the wave generated by a single impact. This was obtained by a side experiment in which we simply dropped from a small height a millimetre sized steel ball in the bath [P12]. We measured the temporal evolution of the resulting wave-field using the Synthetic Schlieren technique introduced by F. Moisy and M. Rabaud [ref 1]. As expected, the local disturbance of a motionless bath generates a radially travelling wave (Film IV.2). If the bath is oscillated vertically at frequency f0 (Film IV.3) the same shock emits the same radial travelling wave, but this wave leaves behind a localized mode of slowly decaying standing waves with a J0 Bessel function profile. These waves are Faraday waves of frequency f0/2. They are sustained during a finite time τ that increases when the amplitude of forcing approaches the Faraday instability threshold.
Computer simulations
The models for walkers have to account for both the wave-field structure and the motion of the drop. Successive models were introduced in reference [P4], [P6] before converging to the version presented in [P12] and [T4]. In this latter version the motion of the drop is determined using the following rules:
1) The drop takes off when the downward bath acceleration exceeds g
2) Once in the air, the drop is in free motion (but can be submitted to an external force)
3) At landing, some of the drop energy is transferred to the bath but this is compensated as it receives a kick in a direction given by the local slope of the interface
4) An additional standing wave is created at the (i+1)th impact.
In order to know the local slope at the point of landing it is necessary to compute the whole deformation of the interface. It results from the linear superposition of Bessel waves emitted at all the previous points of impact. These waves have an exponential temporal decay characterized by the "memory time" τ that depends on the distance to the Faraday instability threshold. This simplified discrete model lends itself to numerical simulations. It is very efficient and reproduces the transition to walking as well as the experimentally observed walker’s dynamics in more complex situations as shown in Films.IV.6 and IV.7. Other models have been proposed more recently [ref 2-4]. They are based on the same general principles but are less schematic from the fluid dynamics point of view. The model proposed by the MIT group relies on a continuous limit approximation.
A pilot wave dynamics
The walker’s wave field being the linear superposition of the successive Faraday waves emitted by past bounces, its interference structure contains a memory of the drop’s recent trajectory. Furthermore, since the travelling waves move faster than the drop, the wave field also contains information about the obstacles that lie ahead. Hence, the spatial and temporal extent of the wave field have two main effects. The past trajectory influences directly the present and the motion is also influenced by waves scattered from distant obstacles. The interplay between the droplet motion and its associated wave field makes this system a macroscopic implementation of a pilot-wave system. The propulsion of the particle by a local gradient due to an associated standing wave is reminiscent of the early de Broglie model for quantum particles, even though no memory effect was considered at that time. The relation to de Broglie model, the existence of chaotic regimes induced by memory effects, and finally the wave-like resulting statistics will be discussed below in part VI.Time reversal
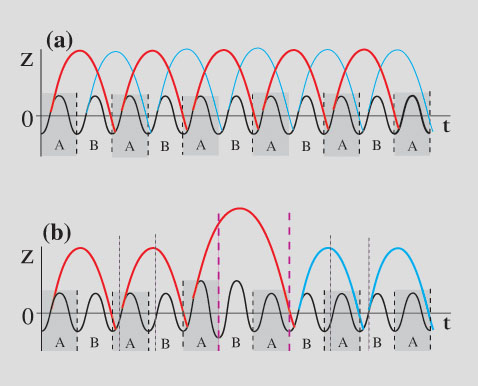
In physics, the time reversal symmetry, i.e. the invariance of the dynamical equations under the transformation t → -t is a general property of conservative systems. But there is a widely studied difference in the temporal reversibility of the dynamics of waves and particles. For waves temporal reversibility is preserved even in the presence of chaos. For particles, as demonstrated in e.g. billiards the temporal reversibility is destroyed in the chaotic regimes by the sensitivity to initial conditions. Is time reversibility restored for a particle dynamics when it is piloted by a wave ? This can be investigated in walkers using one of their specificities [P24] and [T3].In a walker the drop vertical motion is sub-harmonic, it can thus have two different phases relatively to the forcing oscillation. Having chosen arbitrarily a time origin we can distinguish odd and even periods of the forcing oscillation (respectively labeled A and B in Fig. IV-1). In normal conditions, the bouncing is strictly sub-harmonic so that a given drop hits the surface during either the A or the B periods. The emitted waves are also sub-harmonic and temporally synchronized with the bouncing phase of the drop. As sketched on Fig IV-1, by imposing a brief increase in the forcing amplitude it is possible to kick the drop so that it has a single jump lasting three periods instead of two.
A wave-based Turing Machine
From what preceeds it becomes clear that another description of walkers can be given as having a dynamic resulting from an iterative computing process with the following necessary operations processes:
- The system has an internal clock provided by the periodicity TF of the vertical bouncing.
- At each collision with the bath, the drop generates a standing Bessel wave. In this writing process the drop encodes a positionnal information in an extended wave-field.
-Due to the parametric forcing of the wave-field, information is sustained so that the system has a finite time storing process.
-At each new bounce the drop, as it comes in contact with the bath, receives a horizontal kick proportional to the local slope. It corresponds to a reading process in which the stored information determines the drop’s next jump.
To these three basic operations, we have added the existence of the fourth basic elementary operation : the erasing process. As seen above it can be here triggered by an imposed π-shift on the bouncing phase of the drop. The specificity of this iterative machine rely on the way the information is written, stored and processed. Positional information is stored in a global wave field, submitted to the superposition principle of waves. The walker can in that sense be termed as a Wave Turing Machine [P24]. With the possible control of the bouncing phase, the wave memory can be written or erased on demand. This dynamical information storage through a global wave memory can thus be controlled. Even though the present system is unpractical, the finding of similar coupling with waves of a different nature could lead to computing possibilities.
Bibliography
Publications
[P4] Particle-wave association on a fluid interface (PDF)
S. Protière, A. Boudaoud and Yves CouderJ. Fluid Mech. 554, 85-108 (2006)
[P6] Single-Particle Diffraction and interference at a macroscopic scale (PDF)
Y Couder & E.FortPhys. Rev. Lett. , 97, 154101,1-4 (2006)
[P12] Information stored in Faraday waves : the origin of a path memory (PDF)
A. Eddi, E. Sultan, J. Moukhtar, E. Fort, M. Rossi, & Y. CouderJ. Fluid Mech., 674, 433-463 (2011)
[P16] Trajectory eigenmodes of an orbiting wave source (PDF)
E. Fort & Y. CouderEPL, 102, 16005 (2013)
[P24] Wave-based Turing machine: time reversal and information erasing (PDF)
S. Perrard, E. Fort, Y. CouderPhys. Rev. Lett., 117, 094502 (2016)
Theses
[T2] Marcheurs, dualité onde-particule et Mémoire de chemin (PDF)
Antonin Eddi, Thèse de Doctorat de l’Université Paris-Diderot (2 Février 2011)
[T3] Une mémoire ondulatoire : Etats propres, Chaos et Probabilités (PDF)
Stéphane Perrard, Thèse de Doctorat de l’Université Paris-Diderot (29 Septembre 2014)
[T4] Etude d’une dynamique à mémoire de chemin: une experimentation théorique (PDF)
Matthieu Labousse, Thèse de Doctorat de l’Université Pierre et Marie Curie (12 Décembre 2014)References
[ref 1] A synthetic Schlieren method for the measurement of the topography of a liquid interface.
Moisy, F., Rabaud, M. & Salsac, K.Exp. Fluids 46, 1021-1036 (2009)
[ref 2] A trajectory equation for walking droplets: hydrodynamic pilot-wave theory
Oza, A. U., Rosales, R. R. and Bush, J. W. M.J. Fluid Mech. 737, 552-570 (2013)
[ref 3] The pilot-wave dynamics of walking droplets
Oza, A. U., Rosales, R. R. and Bush, J. W. M.Physics of Fluids 25, 091112:1-2 (2013)
[ref 4] Droplets bouncing on a vibrated bath : towards a hydrodynamic pilot-wave theory
Moláček J and Bush J W MJ. Fluid Mech. 727, 612-647 (2013)
