In a walker the motion of a particle is guided by the standing wave generated by the particle itself. This situation is reminiscent of the pilot wave models introduced theoretically by L. de Broglie in an early attempt to account for quantum effects. We can recall briefly recall the history of these models [see P15 & ref].

Pilot waves

In his initial work in 1925, de Broglie [ref 1] proposed for elementary particles (such as an electron) a structure that was meant to account for their dual character. In his model a particle of rest mass m0 has an oscillation at the Compton frequency ν0 = m0c2/h and forms a singular region in a wave field of wavelength λdB=h/mV. This is a standing wave field that results from the superposition of an emitted wave radiated away (retarded wave) and a wave converging towards the particle (advanced wave). The particle is guided by the wave, its velocity being proportional to the gradient of the wave phase. Such an association of the particle to a wave field was meant to introduce the possibility of non-newtonian behaviours. This was summarized by de Broglie in the following terms : "the particle’s motion (...) guided by the wave (...) would not follow the laws of classical mechanics according to which the particle is subject only to the action of forces which act on it along its trajectory, and does not suffer any repercussion from the existence of obstacles which may be situated far away outside its trajectory. In my (. . . ) conception, on the contrary, the movement of the singularity should experience the influence of all the obstacles which hinder the propagation of the wave with which it is connected. This circumstance would explain the existence of the phenomena of interference and diffraction."

Inspired by this work, Schrödinger initially introduced the equation that carries his name while seeking de Broglie’s wave. It was only later that Born demonstrated that the Schrödinger equation was related to the probability of presence. De Broglie then suggested in 1927 [ref 2] that in all quantum systems two wave fields have to be considered.

A first wave-field (that he called u) is generated by the particle. It is a physical wave that has a singularity at its core. (In later versions he proposed that the core region could be strongly non-linear). For de Broglie this wave-particle structure had well-defined trajectories in the physical space. The particle could be submitted to forces but its association to the wave also gave it a non-local sensitivity to the environment and a non-Newtonian behaviour. The second wave-field is ψ the linear and smooth solution of the Schrödinger equation that is related to the statistical density of probability of presence.

Much later, in 1952, David Bohm [ref 3] revisited the idea of a pilot wave and investigated the situation where the wave solution of the Schrödinger equation would be the pilot wave. Bohm used the Madelung transformation of the Schrödinger equation to obtain an equation of motion where a velocity was defined from the gradient of the phase of the Schrödinger wave function. This equation is similar to that proposed by de Broglie, but deceptively so, since these two equations are related to two different wave fields (u and ψ, respectively). In the Bohmian model where the wave function is decoupled from the trajectory itself, a slightly modified Newtonian mechanics can be recovered by addition of a "quantum potential".

The Bohmian trajectories, being computed from Schrödinger’s equation, are necessarily the trajectories of probability densities, rather than those of individual particles. This is the reason for which de Broglie wrote shortly after Bohm’s publication [ref 4] : ". . . David Bohm took up the pilot-wave theory again. His work is very interesting in many ways (...) But since Bohm’s theory regards the wave ψ as a physical reality, it seems to me to be unacceptable in its present form." This led de Broglie to restate in 1959 [ref 5] his "double solution" hypothesis where a wave field u is associated to a given particle and guides its motion.

The recent development of the Bohmian approach has permitted the computation [ref 6], then the experimental observation of trajectories in e.g. interference and diffraction of particle beams [ref 7,8]. Naturally these are trajectories of maximum of probabilities, not those of individual particles. In contrast, little progress was done through the use of de Broglie’s model. The u waves were never detected and it remained unclear how they could generate the random behaviours responsible for the statistics.

As was noted in part III, our system seems a laboratory implementation at macroscopic scale of the idea of the de Broglie type of pilot waves [see P15-P16 & ref 6]. It has however one additional asset absent from de Broglie model : the fact that the wave field contains a memory of the particle trajectory. The previous results, particularly those demonstrating the intermittency phenomena [P20] show that statistical behaviours are observed in this system. Is it possible to go one step further : can wave-like probabilities show-up in our system ? Even though no theoretical model have yet come to demonstrate it, several experiments and numerical simulations, detailed below, show that such is the case.

Confinement

In the experiments presented in section V a force was applied to the droplet. In the experiments to be discussed here no force is exerted directly on to the droplet but its wave-field is disturbed, using sub-marine walls. The propulsion of a walker’s droplet requires that its bouncing triggers Faraday waves. The acceleration needed to reach the Faraday instability threshold depends on the fluid layer thickness, being much larger in shallow regions. For this reason when placed over a submerged barrier, the drop bouncing does not generate those Faraday waves and there is no possible propagation. Therefore such a barrier forms, in principle, an impassable wall for the walker. The three experiments described below use such barriers for confining a walker either partially or totally.


Fig. VI.1. The measured wave field of a walker as it impinges on a submarine wall. The Faraday waves are damped over the barrier

Diffraction and interference

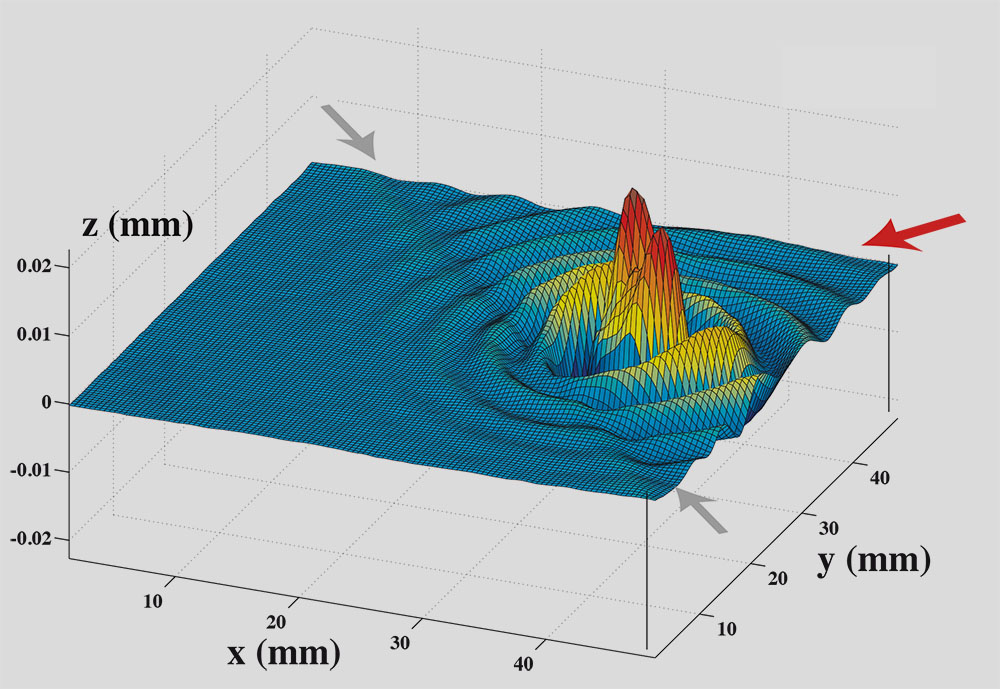
The first question that we addressed [P6] was the following. A walker is formed of an association of a localized object, the drop and an extended structure, the wave. This is a symbiotic association : the waves do not exist if the drop does not generate them and the drop does not move if the waves are damped. When the wave is disturbed for instance by passing through a slit what happens to the drop ? This is why we undertook experiments on the drops trajectories when they pass through apertures limiting the transverse extent of their wave. They were inspired by the founding quantum experiments performed at a low flux of particles. It was shown by G.I. Taylor in 1909 [ref 9] that diffraction or interference patterns could be obtained even when only one single photon was present in the system at a time. These patterns then corresponded to the accumulation of successive individual events and thus reflected a statistical phenomenon. As stated in Feynman’s text-books such results are usually thought to be impossible to understand in a classical way.

The aperture is a slit opened in a submarine barrier. As shown on film VI.1 the drop is deflected. We measured the angle of deflection and found that it was not related in a simple way to the region of the slit the drop had crossed. For this reason we had to do statistics.


Film VI-1 Several crossings of the same slit by the same walker


Fig. VI.2. The deviation of the droplet by a diffraction effect
(a) The deviation of a single walker passing through the slit has no simple relation to its impact parameter in the slit. (b) However if many realizations are done corresponding to an equal flux of particles in all regions of the slit the probability distribution of the deviation angle is related the diffraction of a plane wave through the slit.
It is possible to do a simulation of that phenomenon by assuming that the boundaries are formed of secondary sources so as to guarantee that these boundaries are nodes of the Faraday wave field. As shown by figure VI.3 the resulting trajectories are very complex in the slit region and they result in a probability distribution of the deviations similar to that experimentally observed. It is interesting to note that some trajectories cross the symmetry axis. This is clearly different from the Bohmian trajectories as computed by Philippidis et al. [ref 6] and recently measured [ref 7,8]. These two observations are not incompatible with ours since the trajectories do not concern the same objects.


Fig. VI.3. The trajectories of numerically simulated single walkers passing through a slit (with L/λF=3) (100 evenly distributed incident trajectories)
Discussion

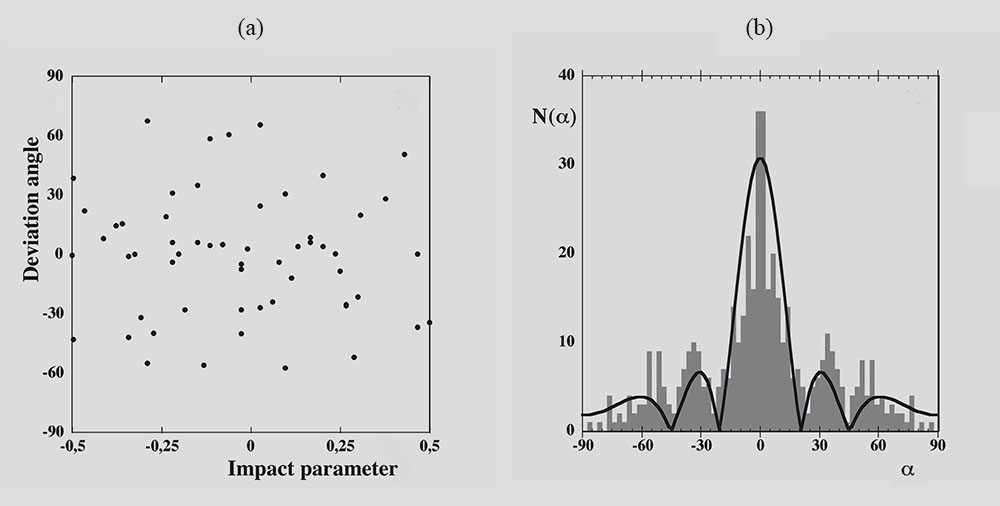
In the present experiment where a similar statistical property is observed its interpretation is simple : while the drop passes through a slit, its pilot wave is sensitive to the whole environment through an echolocation process. Since it is extended in time by memory effects the wave field transfers information to the drop even before it has reached the slit. It is worth noting that several attempts done to repeat this experiment have lead to divergent results [ref 9]. In particular Dan Harris has repeated these experiments in MIT in conditions where the experimental noise is reduced and he does not recover the complex trajectories that we observe both experimentally and numerically in the slit region (see Fig. VI.3). Correlatively his histogram of deviations differs from ours. Obviously more work is needed to understand both the interaction of the walker with the sub-marine boundaries [ref 11] and the role of noise in such experiments.

Tunnel effect

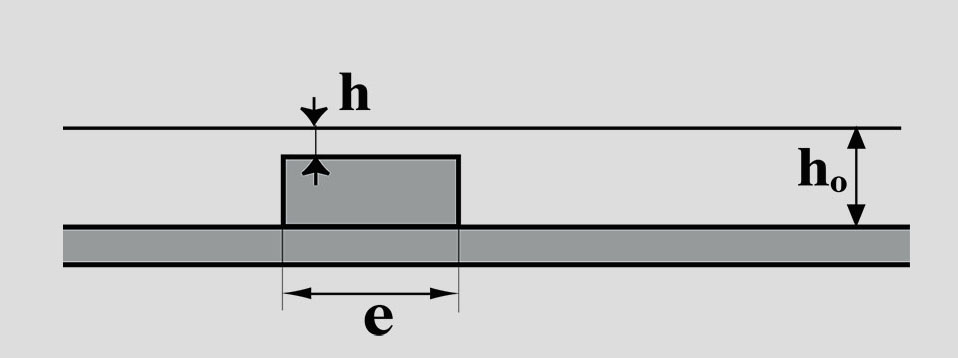
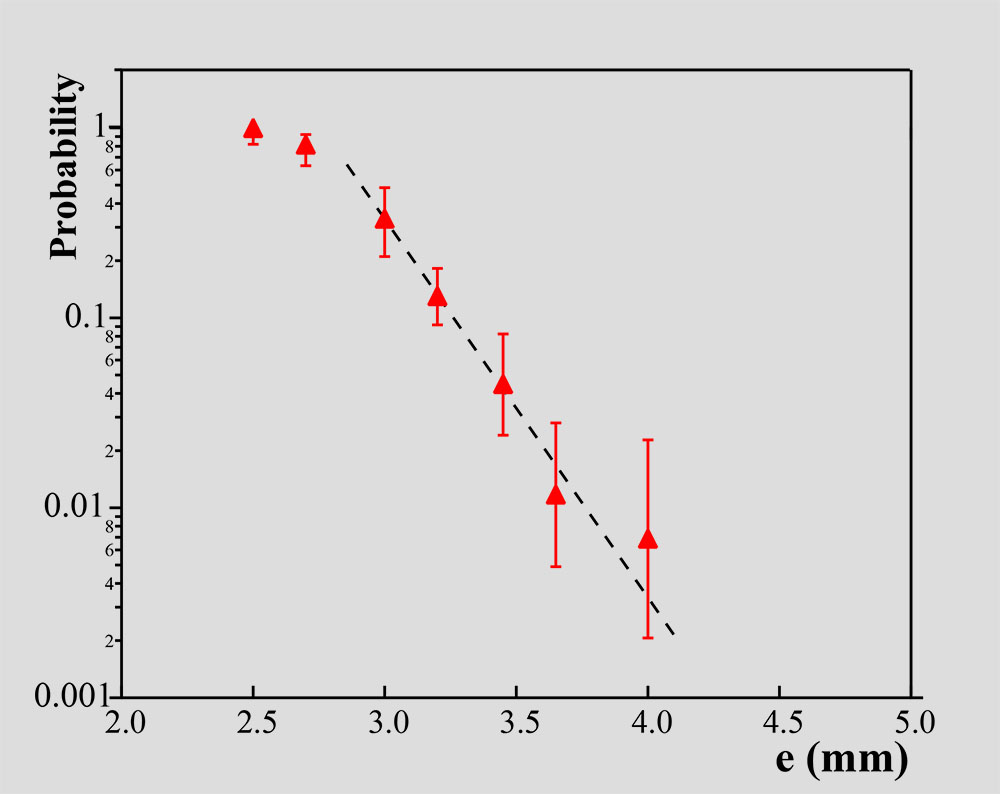
If a walker is enclosed in e.g. a square corral with thick submarine walls, it is trapped with no possible escape as seen in Film VI.2.


Film VI.2. Motion of a walker enclosed in a thick walled corral
However one can wonder if there exists a possibility for a walker to pass through a barrier in which it has no possible walking behavior. We investigated [P9, T2] the motion of a walker trapped in various corrals with walls of small horizontal width e (Fig. VI.5). As directly observed in Films VI.3 and VI.4 the drop does occasionally escape.


Fig. VI.5. Sketch of the submarine barriers used to study the tunnel effect


Film VI.3. Motion and escape of a walker enclosed in a thin-walled corral


Film VI.4. The detail of an escape


Fig. VI.6. The observed trajectories in four square corrals with walls of decreasing thickness
The direct observation of the trajectories reveals that the possibility of escape is related to a change of the typical trajectory inside the corral that becomes increasingly disordered when the walls thickness decreases


Fig. VI.7. Semi-logarithmic plot of the probability of crossing as a function of the thickness e of the barrier
The time needed for the drop to escape in one given realization of the experiment is unpredictable. However a probability of escape can be determined. A systematic investigation of many realizations in various square corrals reveals that this probability decreases exponentially with the wall thickness (see Fig. VI.7). This analogue to the quantum tunnel effect is related to the evanescence of the walking behavior in the shallow regions [P9].

Trajectories in circular corrals

The effect of the confinement of a walker inside a circular corral holds many similarities with the confinement in a potential well that was described in section V.2. This is a non-trivial result since the previous confinement was obtained with a force acting on the drop, while here it is obtained by the effect of the interaction of the waves with the boundaries. At low memory, as shown in film VI.5 the walker follows a circular orbit. In contrast in the high memory regime the trajectory is generally highly chaotic as can be seen in film VI.6. This regime was investigated in a close collaboration with the MIT group headed by John Bush.


Film VI.5. Motion of a low memory walker enclosed in a circular corral


Film VI.6. Motion of the same walker in the same corral but in a long memory situation.
In MIT Dan Harris [P17] built an experimental set-up that allows tuning the excitation extremely close to the Faraday instability threshold. In this regime he registered the walker’s motion during long times. When memory is extremely large the trajectory is strongly chaotic and the velocity of the walker becomes non-uniform. In this regime it is possible, using very long recordings, to measure the spatial distribution of the walker’s probability of presence in a given cavity.


Figure VI.8. Probability distribution of the walking droplet’s position in a circular corral of diameter R = 28.6 mm in which a J0 Bessel mode is at resonance at the Faraday frequency [Dan Harris in P17].
As shown in Fig. VI.8 it has well-defined maxima that are related to the antinodes of the dominant wave eigenmode in the chosen circular corral. In this experiment, as in the diffraction one, a probability wave thus appears when statistical properties of the walker in the chaotic regime are sought (ref 12). We thus obtain a situation, reminiscent of the double solution imagined by de Broglie, in which a physical wave exists that guides the particle while the probabilities of presence have a wave-like behavior [P16]. The possibility to relate these two types of waves is presently actively investigated by e.g T Gilet [ref 10].

Bibliography

Publications

[P6] Single-Particle Diffraction and interference at a macroscopic scale     (PDF)

Y Couder & E.Fort
Phys. Rev. Lett. , 97, 154101,1-4 (2006)

[P9] Unpredictable tunneling of a classical wave-particle association     (PDF)

A. Eddi, E. Fort, F. Moisy & Y. Couder
Phys. Rev. Lett., 102, 240401 (2009)

[P15] Probabilities and trajectories in a classical wave-particle duality     (PDF)

Y. Couder & E. Fort
Journal of Physics , 361, 012001 (2012)

[P16] Trajectory eigenmodes of an orbiting wave source     (PDF)

E. Fort & Y. Couder
EPL, 102, 16005 (2013)

[P17] Wavelike statistics from pilot-wave dynamics in a circular corral     (PDF)

D. Harris, J.Moukhtar, E.Fort, Y. Couder & J. Bush
Phys. Rev. E, 88, 011001 (2013)

[P20] Non-Hamiltonian features of a classical pilot-wave dynamics     (PDF)

M Labousse, S Perrard
Phys. Rev. E, 90 , 022913 (2014)

Thesis

[T2] Marcheurs, dualité onde-particule et Mémoire de chemin     (PDF)

Antonin Eddi, Thèse de Doctorat de l’Université Paris-Diderot (2 Février 2011)

References

[ref 1] Recherches sur la théorie des quanta

de Broglie L.
Annales de Physique , 10-III, 22-128 (1925) - English translation (Kracklauer A.F. 2004)

[ref 2] La mécanique ondulatoire et la structure atomique de la matière et du rayonnement

de Broglie L.
Journal de Physique et le radium , 6-5, 225-241 (1927) - English translation (Kracklauer A.F. 2004)

[ref 3] A suggested interpretation of quantum theory in terms of hidden variables. Part 1 and part 2

Bohm D.
Phys. Rev , 85, 166-193 (1952)

[ref 4] Scientific Papers Presented to Max Born on his retirement from the Tait Chair of Natural Philosophy in the University of Edinburgh

de Broglie L.
Oliver and Boyd (1953) - English translation (Dileep Karanth 2010)

[ref 5] L’interprétation de la mécanique ondulatoire

de Broglie L.
Journal de Physique et le radium , 20, 963-979 (1959)

[ref 6] Quantum interference and the quantum potential

Philippidis C., Dewdney C. and Hiley B. J.
Nuovo Cimento , B52, 15-28 (1979)

[ref 7] Observing the average trajectories of single photons in a two-slit interferometer

Kocsis S., Braverman B., Ravets S., Stevens M. J., Mirin R., P. Shalm L. K. and Steinberg A.M.
Science , 332, 1179-1173 (2011)

[ref 8] Double-slit experiment with single wave-driven particles and its relation to quantum mechanics

Andersen A., Madsen J., Reichelt C., Rosenlund Ahl S., Lautrup, B., Ellegaard C., Levinsen M. T, and Bohr T.
Phys. Rev. E , 92, 013006 (2015)

[ref 9] Interference Fringes with Feeble Light

Taylor G. I.
Proc. Cambridge Philos. Soc. , 15, 114 (1909)

[ref 10] Dynamics and statistics of wave-particle interactions in a confined geometry

Gilet T.
Phys. Rev. E , 90, 052917 (2014)

[ref 11] Non-specular reflection of walking droplets

Pucci G., Saenz P.J., Faria L. & Bush J.W.M.
J. Fluid Mech., 804, R3, 1-12 (2016)

[ref 12] Pilot-wave hydrodynamics

Bush J.W.M
Ann. Rev. Fluid Mech. 49, 269-292 (2015).