Transverse force orbits
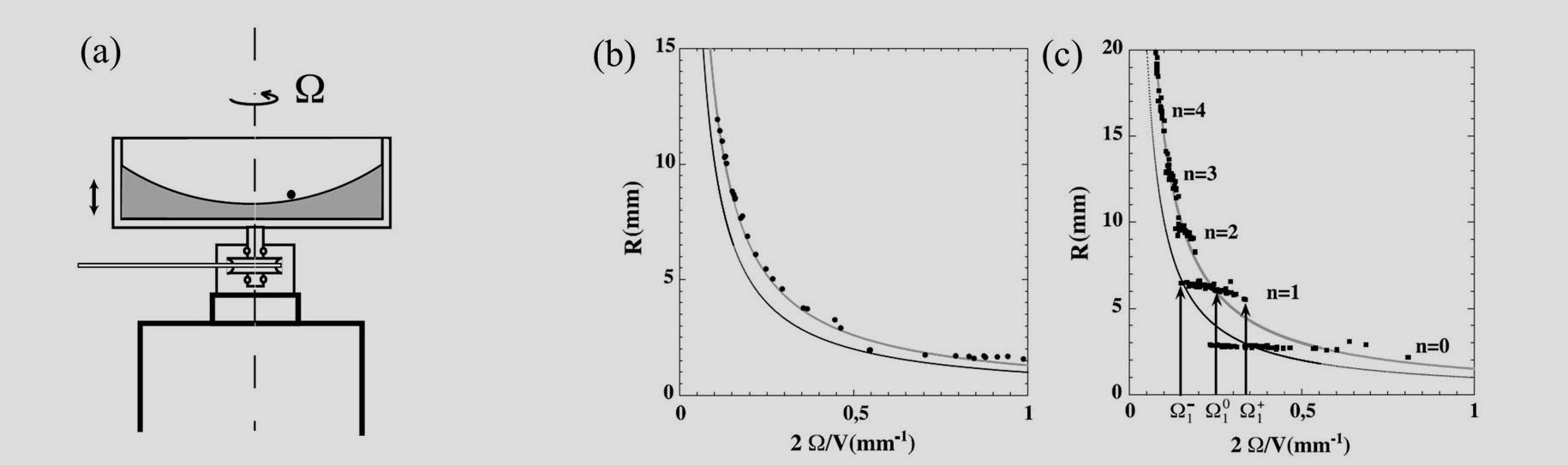
A natural idea to obtain circular orbits was to give the droplet an electric charge and to place it in a magnetic field. If an analogy to quantum mechanics exists we should then observe a form of Landau quantization of the orbits. However, it is difficult to control the electric charge of a droplet so that we turned to a variant. It relies on an analogy first used by Michael Berry [ref 1]. Its starting point is the similarity of relation B=∇×A in electromagnetism with 2Ω=∇×U in fluid mechanics. In these relations, the vorticity 2Ω is the equivalent of the magnetic field B, the fluid velocity U that of the vector potential A. Using this analogy M. Berry found a remarkable hydrodynamic analogue of the Aharonov-Bohm effect (1). Wishing to investigate circular orbits we use the same analogy but differently. A charge q moving at velocity V in a homogeneous external magnetic field B is submitted to FB=q(V × B) . In a system rotating at an angular velocity Ω, a mass m moving with velocity V is submitted to a Coriolis force FΩ=-m(V × 2Ω) where 2Ω is the vorticity of the solid-body rotation. In classical physics, both these forces lead to orbiting motions in the planes perpendicular to B or Ω respectively. In a magnetic field the orbit has a radius ρL=mV / qB. On a rotating surface a mobile of velocity V moves on a circle of radius RC=V / 2Ω.
The two films show a walker of velocity Vw=13.7 ± 0.1 mm/s as it orbits clockwise on a counter-clockwise rotating bath : top Ω= 0.9 Rd/s, bottom Ω= 5 Rd/s.
Central force orbits
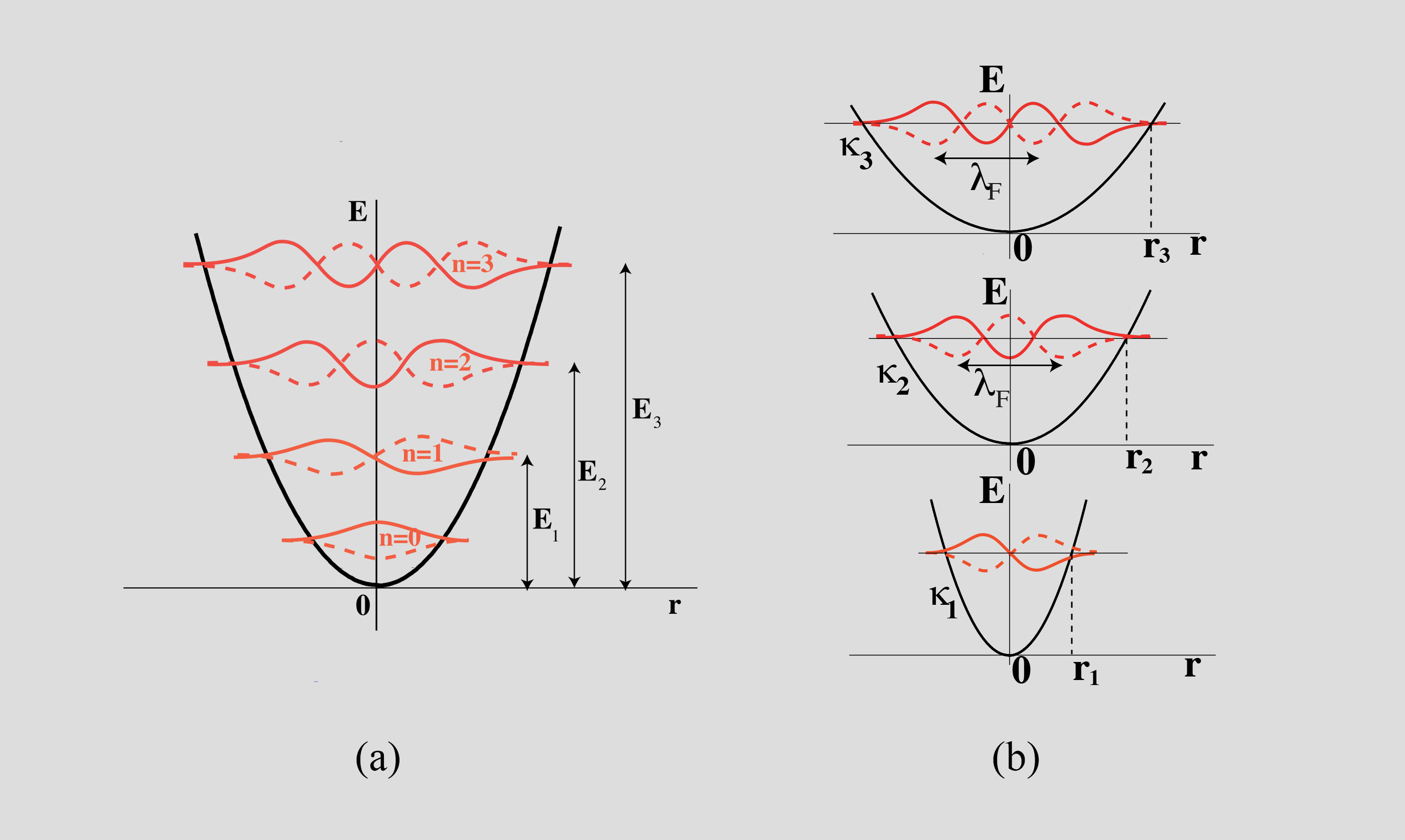
In order to establish the analogy to quantum physics on a firm ground a basic step should be to observe a quantization of energy. Take for instance a quantum particle trapped in a harmonic potential well. It is well known that in quantum physics it can be in successive eigenstates of increasing energy and decreasing mean wavelength as sketched in the one-dimensional case in Fig. 1a. This is unfortunately an experiment that cannot be done with a walker because: the droplet velocity being approximately constant, so is the particle’s kinetic energy. As for the wave field, it is characterized by a fixed wavelength λF. However, it can be noted that in the quantum situation, the successive eigenstates could be obtained at a fixed energy and wave-length by tuning the width of the well (see Fig. 1b). Here we will use this idea to seek the possible emergence of eigenstates when the spatial confinement is varied.
A two dimensional graph can be obtained by plotting against each other
post2.jpg)
In the high memory situations the drop keeps emitting waves in a bounded central region. The accumulation of these waves will necessarily be related to the global wave eigenmodes of this domain. This will have a feedback effect on the droplet motion. The trajectories that eventually emerge are those for which the trajectory shape and the global wave field have achieved a mutual adaptation. We examined the quantization of the mean radii of the various trajectories in this framework. We used a general approach that consists in decomposing (using Graf’s theorem) the entire wave field on the basis formed by the Bessel functions centred on the axis of the potential well. The total wave generates a virtual landscape of wave potential energy that traps the particle in specific orbits. This model [P18, T3, T4] gives an excellent interpretation of the possible radii of the circular orbits: they corresponds to the successive zeros of a J0 function centered on the magnet axis.
The intermittency and the "wave function collapse"
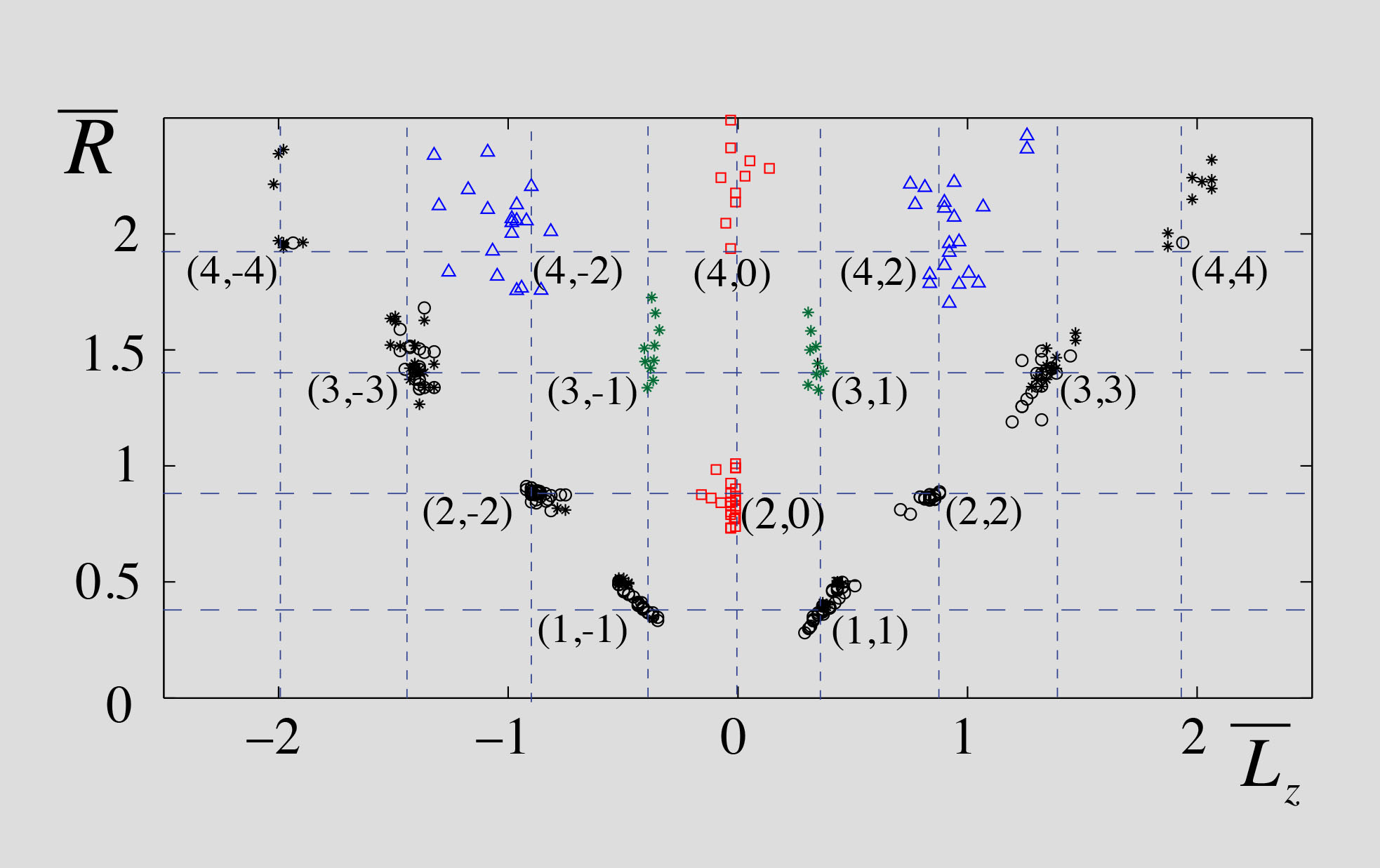
We have thus shown that, as expected from the situation sketched in Figure V.2, there were specific values of the confinement that permitted stable orbital motions. These "states" are characterized by a non-quantum double quantization of the orbit size and the mean angular momentum. Naturally our system has no relation with the Planck constant but, as discussed in [P11], an analogy appears by considering that the Faraday wavelength plays here a role comparable to the de Broglie wavelength in quantum mechanics. We can now examine the motion of the walker when the width Λ of the potential well does not correspond to a pure state.
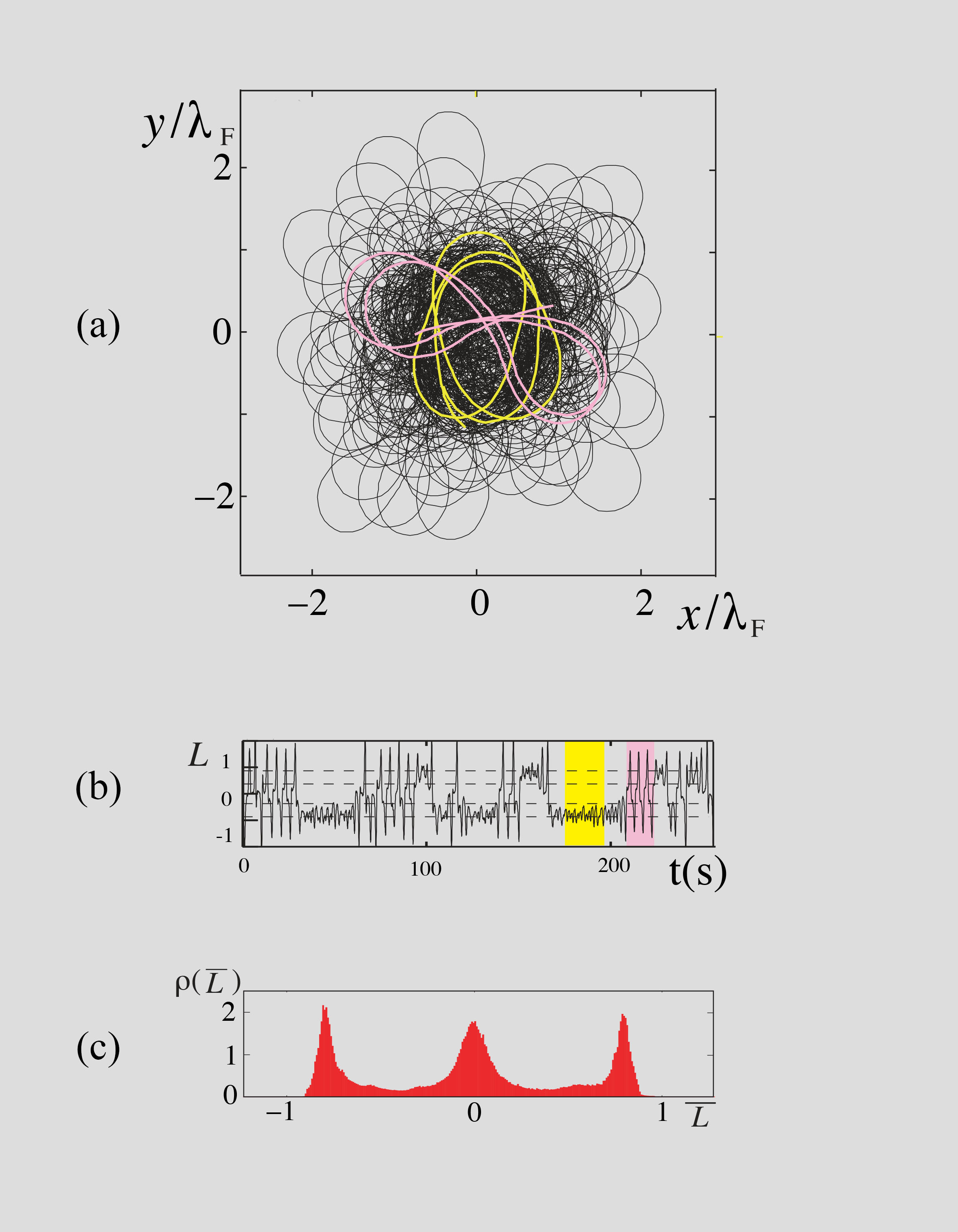
Finally, we can note that we have in this macroscopic system the possibility of performing a continuous non-intrusive observation. It is interesting to consider a gedanken situation in which this observation would be impossible and we could only perform single intrusive measurements. Each of these destructive glimpses would lead to the observation of one of the eigenstates only but they would differ from each other. With many realizations, a probability of each result would emerge. A superposition of states would then be the best reachable description, the probabilities would seem intrinsic and the measurement would appear as a resulting from a "wave function collapse".
Self-orbiting
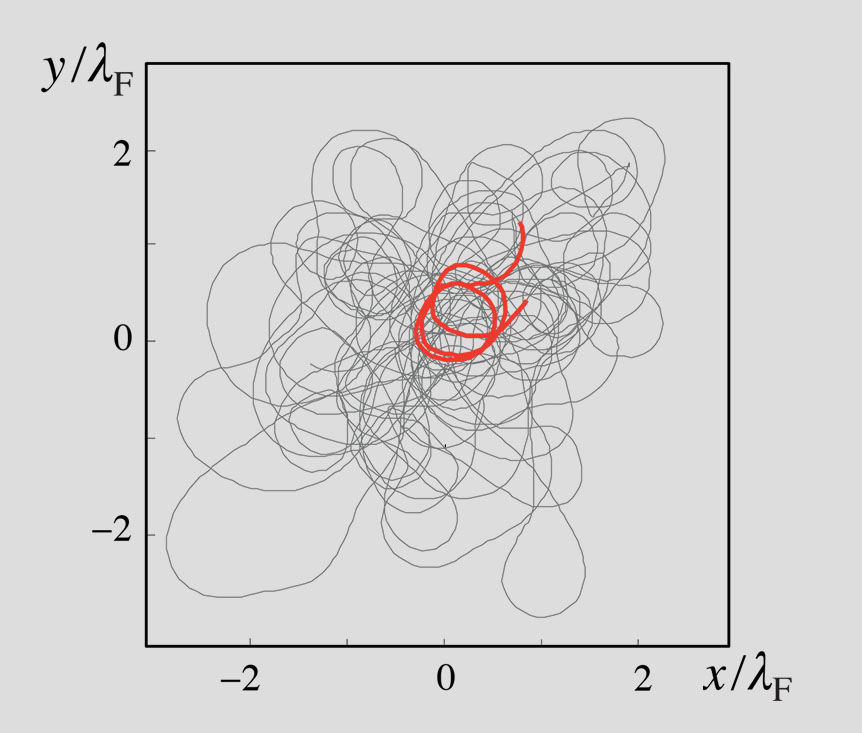
When walkers were discovered, they were observed to move in straight line when undisturbed. One of the questions, raised at that time by Emmanuel Fort, was whether or not this was the only attractor for the drop’s motion. Could there be other states where the interaction with the field led to spontaneous orbiting ? The previously described experiments, in which orbiting is due either to a Coriolis force or to a central force, show that in the high memory regime there is the build-up of an effective wave-induced potential that adds to the trapping. Can this effect be sufficient to produce orbiting ? This was first demonstrated possible by Oza et al. [ref. 3 and 5] in their theoretical investigation of the circular orbits induced by a Coriolis force. However the experimental observation was not possible in that type of experiment. The experimental difficulty in testing this idea is that a "preparation" process is needed to force the walker into a trajectory close to that expected for the self-organized mode so that the corresponding wave field has time to build-up. For this purpose we turned to the central force experiment and used it to set the drop in rotation on a small orbit [P25]. We maintain it in this state during a time longer than the memory time and then switch off the external force. As shown in Figure V.7, the drop keeps orbiting after the switch-off for a time long as compared to the memory time (up to six orbital periods).

Bibliography
Publications
[P11] Path memory induced quantization of classical orbits (PDF)
E. Fort, A. Eddi, A. Boudaoud, J. Moukhtar, & Y. CouderPNAS, 107, 17515-17520 (2010)
[P14] Level splitting at macroscopic scale (PDF)
A. Eddi, J. Moukhtar, S. Perrard, E. Fort & Y. CouderPhys. Rev. Lett., 108, 264503 (2012)
[P16] Trajectory eigenmodes of an orbiting wave source (PDF)
E. Fort & Y. CouderEPL, 102, 16005 (2013)
[P18] Self-organization into quantized eigenstates of a classical wave-driven particle (PDF)
S. Perrard, M. Labousse, M. Miskin, E.Fort, & Y. CouderNature Com, 5, 3219 (2014)
[P19] Chaos driven by interfering memory. (PDF)
S. Perrard, M. Labousse, E. Fort, Y. CouderPhys Rev Lett, 113, 104101 (2014)
[P20] Non-Hamiltonian features of a classical pilot-wave dynamics (PDF)
M Labousse, S PerrardPhys. Rev. E, 90 , 022913 (2014)
[P21] Build-up of macroscopic eigenstates in a memory based constrained system (PDF)
M. Labousse, S. Perrard, Y. Couder and E. FortNew Journal of Physics, 16, 113027 (2014)
[P23] Pilot wave dynamics In a harmonic potential: Quantization and stability of circular orbits. (PDF)
M. Labousse, A.U. Oza, S. Perrard, J.W.M. BushPhys. Rev. E, 93, 033122 (2016)
[P25] Self-attraction into spinning eigenstates of a mobile wave-source by its emission back-reaction
M. Labousse, S. Perrard, Y. Couder & E. FortPhys. Rev. E. (to appear 2016)
Theses
[T2] Marcheurs, dualité onde-particule et Mémoire de chemin (PDF)
Antonin Eddi, Thèse de Doctorat de l’Université Paris-Diderot (2 Février 2011)
[T3] Une mémoire ondulatoire : Etats propres, Chaos et Probabilités (PDF)
Stéphane Perrard, Thèse de Doctorat de l’Université Paris-Diderot (29 Septembre 2014)
[T4] Etude d’une dynamique à mémoire de chemin: une experimentation théorique (PDF)
Matthieu Labousse, Thèse de Doctorat de l’Université Pierre et Marie Curie (12 Décembre 2014)
References
[ref 1] Wavefront dislocations in the Aharonov-Bohm effect and its water wave analogue
Berry MV, Chambers RG, Large MD, Upstill C, Walmsley JCEur J Phys 1, 154-162 (1980)
[ref 2] Droplets walking in a rotating frame: from quantized orbits to multimodal statistics
Harris D M and Bush J W MJ. Fluid Mech. 739, 444-64 (2013)
[ref 3] Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization
Oza A U, Harris D M, Rosales R R and Bush J W MJ. Fluid Mech. 744, 404-29 (2014)
[ref 4] The wave-induced added mass of walking droplets
Bush, J.W.M., Oza, A. & Moláček JJ. Fluid Mech. 755, R7 (2014)
[ref 5] Pilot-wave dynamics in a rotating frame: Exotic orbits
Oza, A., Wind-Willassen, O., Harris, D. M., Rosales, R.R. and Bush, J. W. M.Phys. Fluids 26, 082101 (2014)
[ref 6] Faraday pilot-wave dynamics: modelling and simulation
Milewski, P.A., Galeano-Rios, C.A., Nachbin, A. and Bush, J.W.M.,J. Fluid Mech. 778, 361-388 (2015)